Understanding the Math Equation of a Circle
Before we jump to the code, let's get a small lesson on how are circles represented in a polar coordinate system.
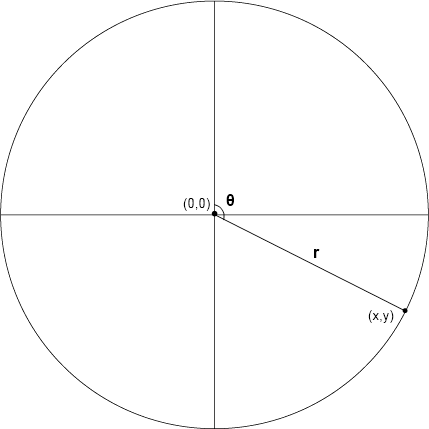
Imagine a circle with a radius r at the Origin. The circle's center can be depicted as (0,0) and (0,r) is a point on the circle.
Another way to represent this point on the circle would be
𝑥=𝑟 sin 𝜃, 𝑦= 𝑟 cos 𝜃
Here 𝜃 is the angle in radians.
Now that we know how to represent a point on the circle, let's translate this into some Kotlin code.
Writing the Code
fun printPointOnTheCircle(thetaInDegrees: Float, radius: Float, cX: Float, cY: Float) {
val x = cx + (radius * kotlin.math.sin(Math.toRadians(thetaInDegrees)).toFloat())
val y = cY + (radius * kotlin.math.cost(Math.toRadians(thetaInDegrees)).toFloat())
println("(x,y) = ($x,$y)")
}Behind the Scenes
💌 A special section on my blog for ️️my subscribers❤️.
Here I share how did I come up with the idea for this article.
It could be inspirational, motivational, or quirky but definitely not traditional
because it was born out of my hustle.
The idea for this blog came up when I was writing a blog about coding Custom Progress Bar with Jetpack Compose Canvas API. Here is what I was trying to achieve.

While the mathematical equation for a point of a circle was straightforward to remember. I still had to tailor it a bit, to position the white dot accurately in the arcs. This is because the coordinate system of android has its origin based on the top-left corner and not the actual center of the screen.
I drafted the whole process by hand, here are the notes with visual illustrations to show you how I approached the problem.